Harnesses, Carts and Carriages

Unfortunately harnessing has often been of minor interest in cattle hitching, although actually it should be of highest priority to ensure comfortable and efficient draft power transfer. Throughout history there have been many ways to hitch cattle, with many different systems being used side by side or competitively. Nowadays we prefer harnessing with the 3-pad-collar of Steinmetz (see literature). It is the optimal way of harnessing cattle. It adapts to the particular anatomy and motion of pulling cattle, is very flexible and extremely efficient. The core piece consists of a collar with three upholstered pads (Kummet). Traction is transferred at the mobile shoulder blades (scapulas) of the animal via the collar pads and to some extent at the withers with the smaller third pad. Because the collar can flex and move, the draft power transfer does not interfere with the cattle's natural motion. Moreover, the angle of traction can be kept level, thus increasing the efficiency of tractive output. The tugs are attached to the collar.
Depending on single or team hitching, the harness is fixed by a girth. Carts and carriages can be slowed by chains hooked to the pole or by breeching fixed to the shafts.
Nowadays it seems to be rather a challenge to find good quality cattle harnesses. Most of those available are rarely complete, of poor quality and quite often useless (leather chapped and therefore not comfortable or resilient). At best they serve as patterns for new ones, or as decoration only. There are almost no saddlers left who are willing or able to fabricate these kinds of harnesses. One is left with the search for a saddler in the hope of being able to talk him into possibly making a new collar or even a complete harness.
Literature: "Modernes Geschirr für Arbeitsrinder" / Modern Harnesses for Working Cattle by Rolf Minhorst
We are keen to encourage saddlers, leatherworkers or any person interested in this topic to contact us, in order to fulfill this market need!!
Draft Animal Conformation
A Veterinarian’s Viewpoint. (Original article in AIMA)
by Barbara Corson
An extremely important contribution, it explains many differences in the possible harnesses and hitching types, not only in cattle but also in contrast to the horse!
Physics of an Evener
The points of draft for the load (in the centre) and the animals (at either end) are either in a straight line or form a triangle, with the load behind or in front of the animal draft points.
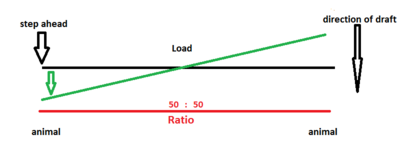
For now, consider an evener where the point of draft for the load is dead center. It is effectively between 2 equally long levers.
If all 3 draft points are in a row, both animals pull the same weight, regardless of their place during the pull; they pull half of the total load each at any time.
Work = Force x Distance
also valid:
Force1 x Distance1 = Force2 x Distance2
now we assume a load of 500kg, which both animals have to move together
Force1 + Force2 = 500kg
this can be inserted in the upper equation:
F1 x D1 = (500kg-F1) x D2
F1 x D1 = 500kg x D2 - F1 x D2
F1 x D1 + F1 x D2 = 500kg x D2
F1 = 500kg x D2
D1+D2
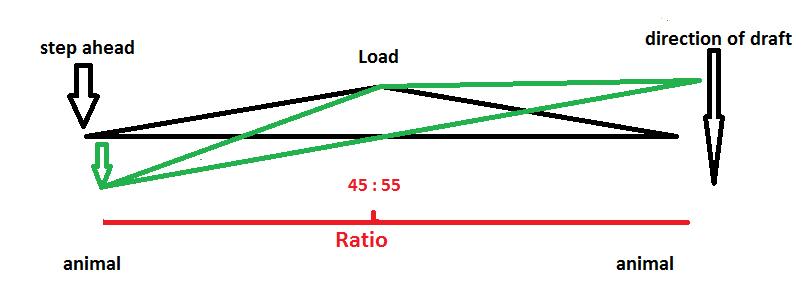
But what happens, when the point of draft for the load moves behind the connecting line between the 2 points of draft for the animals?
As an example, consider an evener with levers of 55cm each and where the center point of draft for the load is 15cm behind the connecting line of both ends of the evener
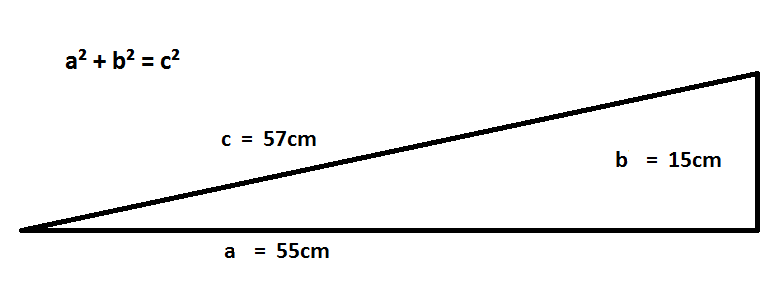
a² + b² = c²
a = 55cm (length of levers)
b = 15cm (distance of point of draft from connecting line of evener's ends)
c = line connecting point of draft of load to the points of the animals
55² + 15² = c²
3025 + 225 = 3250 this implies : c = 57cm
Keeping the same 500kg load as an example, there is still an equal load split of 250kg for each animal, if the evener is at a right angle to the direction of the draft (i.e. both animals stay exactly side by side).
F1 = 500 x D2
(D1 +D2)
F1 = 500 : 2 (because at a right angle D1 and D2 are equal)
= 250kg
But what happens if the left animal steps ahead exactly 15cm?
the situation on the right: a2 = c2 und b2 = 0
on the left: a1 x a1 + b1 x b1 = c1 x c1
a1 x a1 + 30 x 30 = 57 x 57
a1 x a1 + 900 = 3250
a1 = 48,48cm a2 = 57cm
F1 x D1(equivalent to a1) = F2 x D2(equivalent to a2)
F1 = 500 x 57 : 105,48 = 270kg F2 = 230kg
...
What are the numbers if we harness 2 animals of different size and therefore use an evener with 2 different levers, the longer 55cm, the shorter 50cm (that would compensate for an animal of about 950kg versus one of 1050kg)?
The smaller animal at the longer lever steps ahead 25cm and still has to pull a load of 279kg, while the heavier animal on the short and further behind lever still has to pull 221kg.
The other way around: the animal at the short lever pulls ahead: with a step of a mere 25cm there is a difference of 134kg to the other side, enormous considering a total of 500kg.
It is fascinating how a few cm can produce such an enormous difference in pull - load for the single animal and some levers allow for just these changes both in the center and at one end.
We should definitely use these possibilities for the reduction of workload and the welfare of our animals!
